Eine dynamische Geometriesoftware, zum Beispiel GeoGebra, ist spätestens ab Klasse 8 verbindlich im Bildungsplan Mathematik verankert. In diesem Zusammenhang bietet sich an, Konstruktionen mit GeoGebra anhand des Satzes von Thales zu vertiefen oder einzuführen. In dynamischer Weise haben die SuS so die Möglichkeit den Satz des Thales selbstständig zu entdecken und erste Vermutungen aufzustellen.

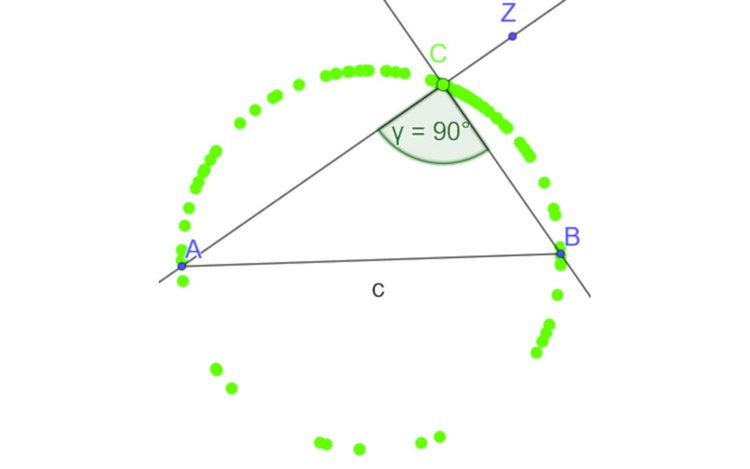
Die Unterrichtssequenz ist so aufgebaut, dass die SuS im ersten Schritt mittels der "Schulhof-Aufgabe" einen handlungsorientierten Zugang (enaktiv) zum Satz des Thales finden. Sie erleben und diskutieren Beobachtungen bezüglich der Eigenschaften von Dreiecken, dessen Eckpunkte den Durchmesser eines Kreises bilden und dessen dritter Eckpunkt auf dem Kreis liegt. Im zweiten Schritt haben die SuS die Möglichkeit, ihre Konstruktion vom Schulhof mit der dynamischen Geometriesoftware GeoGebra nachzuvollziehen (ikonisch) und ihre bereits gemachten Beobachtungen genauer zu untersuchen und zu formalisieren (symbolisch). In Einzel- oder Partnerarbeit (je nach technischer Ausstattung) werden die Konstruktionsaufgabe sowie weiterführende Aufgabenstellungen bearbeitet. Geschieht die Bearbeitung in Einzelarbeit, so können sich die SuS mittels der Bus-Stop-Methode oder nach maximal 30 Minuten mit einem Partner zu einer Austauschphase, in der sie die Ergebnisse vergleichen und diskutieren, zusammenfinden. Falls SuS auch mit dem Austauschen deutlich eher fertig sind, könnten sie sich mit der Umkehrung des Satzes von Thales auseinandersetzen. Der Austausch bietet allen SuS eine Grundlage, um im Plenum ihre Ergebnisse vorzustellen und ihr Wissen zu vertiefen.
Damit die SuS entsprechend ihrer Neigungen und Fähigkeiten gefördert werden können, gibt es verschiedenartige Hilfsmaterialien, die den SuS während der Bearbeitungszeit zur Verfügung gestellt werden. Wenn es allgemein Schwierigkeiten im Umgang mit GeoGebra gibt, können die SuS die Informationen "Tipps zum Umgang mit GeoGebra am Computer/ Laptop" nutzen. Diese Informationen sind leicht auf den Umgang mit GeoGebra am Smartphone oder Tablet zu übertragen. Haben die SuS Schwierigkeiten beim Verstehen der Konstruktionsbeschreibungen bzw. bei der entsprechenden Auswahl der GeoGebra Werkzeuge, dann können sie zwischen verschiedenen Hilfekarten wählen. Bestehen Probleme bei der Formulierung der Vermutungen (symbolisch) der gewonnenen Erkenntnisse, so steht im Sinne eines sprachsensiblen Unterrichts eine Hilfekarte mit Formulierungsvorschlägen zur Verfügung. Auf die korrekte Benennung der mit GeoGebra konstruierten Eckpunkte, Seiten, Geraden etc. kann ggf. verzichtet werden, um die SuS nicht zu überfordern. Im Plenum könnte erläutert werden, warum GeoGebra wie welche Objekte benennt und wie diese umbenannt werden können (siehe dazu Informationsblatt zu GeoGebra). Je nach Gewohnheit, können die SuS ihre Konstruktion und Vermutungen/Hypothesen digital speichern bzw. sichern oder sie übertragen die Konstruktion mit den zugehörigen Vermutungen in ihr Heft. Es wird nicht erwartet, dass in der Einzel- bzw. Partnerarbeit alle SuS ihre Beobachtungen verschrifltichen bzw. ihre Vermutungen dem Satz des Thales entsprechen. Wichtig ist, dass sie das Werkzeug GeoGebra kennenlernen, bisherige mathematische Kenntnisse zu Dreiecken und Winkeln auffrischen und zumindest mit dynamischen Veränderungen ihrer Konstruktion erste Beobachtungen mit Blick auf den Satz des Thales machen.
Die Ergebnisse werden abschließend im Plenum zusammengetragen, ergänzt und vervollständigt und vertieft. Eine Reflexion über den Zugang zum Satz des Thales sowie den Umgang mit GeoGebra schließt diesen Teil ab.
Im weiteren Verlauf der Unterrichtseinheit könnten die SuS je nach Neigung und Interesse entweder den Beweis des Satz des Thales, die Umkehrung des Satzes (und dessen Beweis) oder Anwendungsaufgaben (Konstruktionsaufgaben, Blickwinkel) anhand des Buches / Internets recherchieren und erarbeiten. Abschließend könnten die gewonnenen Erkenntnisse ebenfalls mit GeoGebra den MitschülerInnen zum Beispiel in einem (digitalen) Gallery Walk (z.B. Padlet, Book Creater) präsentiert werden.

Nachdem die SuS bereits im Bereich der Leitideen "Messen" und "Raum und Form" Winkel und Dreiecke klassifizieren und händisch geometrische Figuren konstruieren können (ggf. schon mit einer DGS), wenden sie ihr erlerntes Wissen an und entdecken den Satz des Thales. Die SuS schätzen und messen Winkelgrößen, dabei nutzen sie die Genauigkeit der dynamischen Geometriesoftware. Sie konstruieren und zeichnen geometrische Figuren (auch) unter Verwendung einer dynamischen Geometriesoftware und klassifizieren geometrische Objekte (Winkel, Dreiecke). Darüber hinaus können weitere Kompetenzen, wie das gedankliche verändern von Objekten in ihrer Lage, Größe und Form (Kopfgeometrie), trainiert werden. Der fachliche Fokus der Einheit liegt auf der Konstruktion von Figuren mit einer DGS sowie dem mathematischen argumentieren und kommunizieren (vgl. Bildungsplan Gymnasium Sekundarstufe 1. Mathematik. 2011).

Differenzierungsmöglichkeiten sind vielfältig mittels Hilfekarten sowie verschiedenen Teilaufgaben, die nicht von allen gelöst werden müssen, gegeben. Darüber hinaus wäre es möglich, neben diesen Materialien sehr leistungsschwachen SuS einen digitalen Lernpfad zur Verfügung zu stellen (siehe weiterführende Links), so dass diese SuS wenige / bis keine eigenständigen Konstruktionen mit GeoGebra erstellen, sondern nur Konstruktionen nutzen, um Beobachtungen die zum Satz des Thales führen sollen, zu machen. Es sind verschiedene Erweiterungen denkbar: Geometrischer Beweis des Satz des Thales, die Umkehrung des Satzes und der Beweis, Problemlöse-Aufgaben (Konstruktionsaufgaben auf verschiedenen Niveaus - z.B. Punkt außerhalb eines Kreises ist gegeben und eine Tangente soll an den Kreis konstruiert werden, Blickwinkel).

Falls nach dem handlungsorientierten Zugang (Schulhof-Aufgabe) leistungsstarke SuS den Satz des Thales schon formulieren, könnte ihnen an dieser Stelle die Möglichkeit gegeben werden, die Umkehrung des Satzes mit GeoGebra zu betrachten oder den Satz des Thales zu beweisen. Weitere detaillierte Hinweise und Tipps finden sich in der Verlaufsplanung.